De: La Frikipedia, la enciclopedia extremadamente seria. De: La Frikipedia, la enciclopedia extremadamente seria.
Faraday desconocía por completo el cálculo diferencial, y probablemente muchos de vosotros desconozcáis el integral. Esta pequeña guía os servirá para que adquiráis los conocimientos básicos sobre el cálculo de primitivas, y así podáis continuar con vuestras investigaciones y aportes en la Matemática y la Ciencia.
Por el Principio Socrático de Definición, no podemos hablar de integrales sin saber lo que es una función. Una función es un especimen matemático que mediante una serie de operaciones (aritméticas, trigonométricas…) hace corresponder valores entre espacios, bien se trate de una o varias variables. En la práctica y si contamos con la gráfica, lo que nosotros haremos para saber si es de una función es aplicar los siguientes pasos:
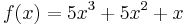
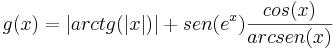
¿A quién le interesa la definición de integral? A nosotros no, ya que las consideramos como algo que queremos quitarnos del medio lo antes posible. Entramos en conflicto con el mencionado Principio Socrático de Definición, pero qué remedio. Limitémonos a lo que nos interesa.
Sin ninguna complicación, llevamos a cabo los siguientes pasos:
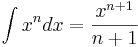
Sólo lo haremos si es factible.
Aplicamos la regla mnemotécnica que tanto fastidia a los matemáticos ortodoxos.
<<Sole, un día vi un valiente soldado vestido de uniforme>>.
.
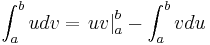Una vez deducida la igualdad, hemos de estudiar la naturaleza de la función para ver quién es u y quién es dv.
Existen otros métodos que a nosotros no nos interesan. Si no sale ni por cambio de variable ni por partes, lo que haremos será llevar el cambio de variable a un estado extremo, al aplicar el siguiente algoritmo:
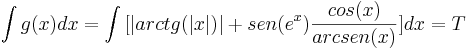
Nota: Se ha demostrado empíricamente que este método sólo resulta efectivo si dominamos los límites, continuidad, derivación, y representación de funciones. Los resultados son sorprendentes, así que hacedme caso y tratad a los pasteles que se os presenten como lo que son, pasteles. La mejor forma de evitar que se recurra a este método es planteando ejercicios de sólo integración.
Analicemos un volumen de control cualquiera, por ejemplo (así al azar), una de las turbomáquinas del Slit-X Collor Pondrat Plug-F Mamothuna. Bien se sabe que la temperatura de estos ingenios aumenta considerablemente cuando se mete el turbo, y que tal aumento puede provocar daños severos en los materiales que los componen. Resulta interesante, por tanto, calcular el calor cedido al ambiente una vez transcurrido el enfriamiento post-turbo.
Aplicando la ecuación de conservación de la energía:
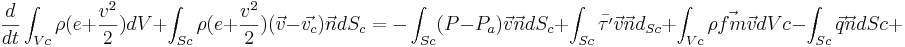
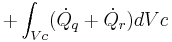
Y realizando las siguientes consideraciones:
La mitad de las integrales se van, literalmente, a freír espárragos, resultando:
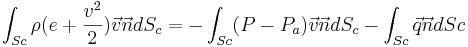
Las dos primeras integrales se resulven sin dificultad particularizando en la superficie de entrada y en la de salida. El problema está con la tercera. ¿Cuál diantres es la normal de la tercera integral? Si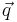 
es un vector... ¿cuáles diantres son sus dichosas coordenadas? ¿Cómo se supone que debemos integrar eso? ¡No hay problema! Aplicamos el algoritmo arriba mencionado.
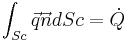
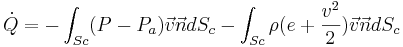
La pregunta es si merece la pena mandar a Terminator al pasado para matar a Newton. ¿Son realmente necesarias estas artimañas matemáticas para el desarrollo del ser humano? Las civilizaciones antiguas levantaron sus templos y edificios sin siquiera la recta real, pero qué hay de la fusión nuclear o de los aceleradores de partículas.
Autor(es):
